刘志强、罗义力

近邻传播聚类算法(Affinity Propagation，简称AP)由Frey和Dueck [1]在2007年提出：

· 每个点都看作是潜在的聚类中心，不需要用户明确指定聚类个数和初始化中心，避免了初始类中心对聚类结果的影响；

· 可以使用任意距离度量方式，不需要满足三角不等式和距离对称性条件，这些特点让它可以很好地解决非欧空间问题。

1、概念介绍：

· 相似度：表示点j作为点i的聚类中心的能力，记为s(i, j)。一般使用负的平方欧几里得距离，值越大表明相似度越高；

· 相似度矩阵：N个点之间两两计算相似度形成的矩阵，记为s；

· 偏向参数(Preference)：点i作为聚类中心的参考度，记为p。相似度矩阵对角线的值会被设为该值，值越大，为聚类中心可能越大；默认是取相似度矩阵的中位数（可以生成适当个数的聚类）；

· 吸引度(Responsibility)：指点k适合作为数据点i的聚类中心的程度，记为r(i,k)；

· 归属度(Availability)：指点i选择点k作为其聚类中心的适合程度，记为a(i,k)；

· r (i, k)和a (i, k)的值越大，则点i选择点k作为聚类中心的可能性越大，点k作为聚类中心的可能性也就越大。

 2、计算流程：

Scala代码通过breeze实现矩阵的迭代更新部分，如下图所示。其对应sklearn中AP算法路径为https://github.com/scikit-learn/scikit-learn/blob/1495f6924/sklearn/cluster/affinity_propagation_.py#L156-L188 

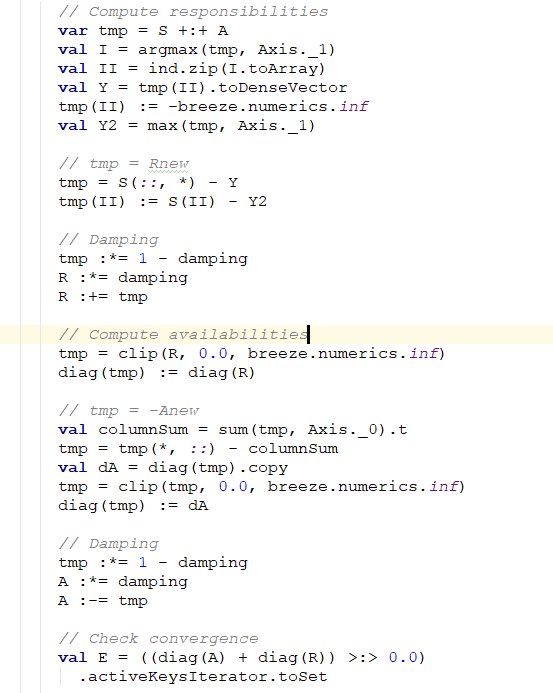
3、并行化思路：

因为近邻传播需要计算相似度矩阵，所以在大规模数据下性能很差。本文实现Spark下的近邻传播算法基于DisAP[2]算法（Distributed Affinity Propagation Clustering Based on MapReduce），基本的执行流程如下：

· 将输入数据集随机划分为S个大小为partitionSize的小数据集{D1,D2,…,DS}；

· 在每个小数据集Di上运行一次AP算法得到若干个代表点，重复执行，直到所有代表点的规模小于阈值N；

· 将所有代表点集中在一台Worker机器上再运行一次AP算法，得到最终的代表点；

· 最后为每个点选择最近的代表点；

Spark实现代码如下：

DisAP算法的理论依据是：假设第一次聚类得到的代表点，保持了原数据的分布，如果获取的代表点足够多的话，对聚类代表点进行聚类得到的新代表点对原数据集依然有很强的代表性。但是算法忽略了不同分区的数据集的点之间的相似度，实际上是在一个稀疏图上进行计算，是一种近邻传播的近似算法。

4、实验效果：

我们使用标准化互信息(Normalized Mutual Information，简称NMI)作为外部指标考察聚类准确性，NMI取值范围为[-1，1]，并且越接近1，表示聚类效果越好。我们在四个数据集下对比了DisAP算法和KMeans算法的聚类效果，详细的NMI值如下表所示：

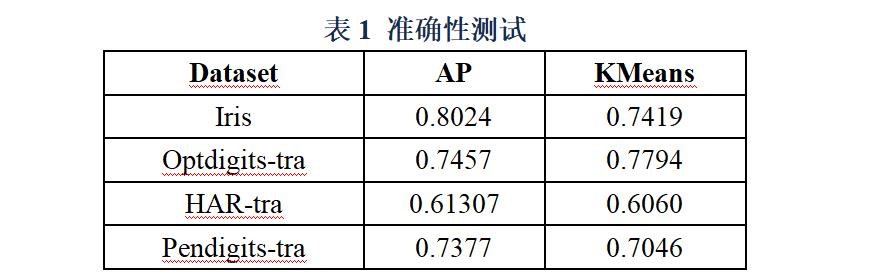
从测试结果可以看出，KMeans和DisAP表现各有胜负。两种算法在现实数据集上的NMI值都不是特别高，主要原因有：1)参数尚未调整到最优，并未达到最好的聚类效果；2)在欧氏空间并不能很好地分类数据。

下图是Spark DisAP算法和sklearn实现的AP、Kmeans算法的实现效果的对比，可以看出，DisAP只是AP算法的近似分布式实现，聚类效果还是有差异的。

KMeans每次迭代的时间复杂度为O(NK)，其中N表示数据规模，K表示期望的聚类个数，而近邻传播算法每次迭代需要交替更新吸引度矩阵R和归属度矩阵A，时间复杂度为O(N²)，一般来说K远小于N，因此近邻传播算法的时间复杂度几乎比KMeans高一个数量级。在分布式条件下，尽管我们对近邻传播算法进行了并行化处理，DisAP的运行效率仍然逊色于并行化方法更为成熟的KMeans。

总结：

本文在Spark上实现了近邻传播的分布式算法DisAP，并在4个数据集获得了不逊于KMeans的准确性。相对于KMeans聚类，DisAP算法可以不需要设置聚类个数，但是DisAP算法需要设置偏向参数preference（控制聚类个数），阻尼系数damping，缩放因子scale等，调优工作量相对KMeans来说更大。此外，从执行效率上分析，DisAP算法需要计算分区数据的相似矩阵，并且大数据情况下，需要多次数据shuffle，计算性能远不如KMeans算法。

参考文献

[1]Brendan J. Frey and Delbert Dueck. Clustering by passing messages between data points. Sci-ence, 315:2007, 2007.

[2]Lu W, Du C, Wei B, et al. Distributed Affinity Propagation Clustering Based on MapReduce[J]. Journal of Computer Research & Development, 2012, 49(8):1762-1772.