

2019-07-22
分享到王肇康、胡卫薇、顾荣
本篇将分享江苏鸿程大数据技术与应用研究院图计算技术组最近在图数据查询方向的最新工作。
该工作的论文最近发表在数据库领域的顶级国际学术会议ICDE 2019上,会议论文可以从IEEE论文数据库中获取。
图(Graph)是一种很适合描述现实世界中的对象和对象之间关系的数据结构,例如社交网络就是一种典型的图结构。社交网络中的人对应于图中的顶点(Vertex),人与人之间的联系对应于边(Edge)。

图1:社交网络可以用图数据结构表达
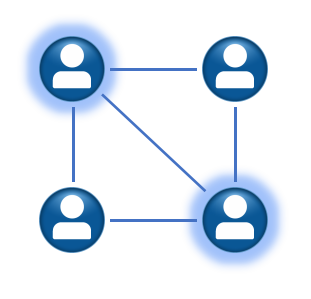
图2:一种4人小团体结构
子图匹配(subgraph matching)就是在一个数据图(data graph)中查找出用户给出的模式图(pattern graph)的实例的过程。以社交网络为例,下图展示了一个4人小团体,小团体中核心的两个人互相是朋友,而且他们还有两位共同好友。小团体中目前不认识的两个人将来很可能成为朋友。给定一个很大的社交网络,从社交网络中找出具有上述小团体结构的子图的过程,就是子图匹配。社交网络对应于数据图,而小团体结构就是我们感兴趣的模式图。图1中虚线框标示出了在社交网络中找到的小团体结构。子图匹配作为图数据结构上的高级查询操作,在图数据库、社交网络推荐、生物功能网络分析等诸多领域都有广泛应用。
形式化地,一张图g是由顶点集V(g)和边集E(g)所定义的数据结构,g=(V(g),E(g))。本文中我们假设处理的图都是边没有方向的无向图。给定一张数据图G和一张模式图P,子图匹配即是从G中找出所有与P同构的子图。图3中展示了一个示例的数据图G和模式图P,数据图中与模式图同构的子图(即匹配的子图)用粗线条标示。在数据图中找出所有的匹配子图的过程,称为子图枚举(subgraph enumeration)。本工作即关注如何在分布式计算环境中高效地实现子图枚举。
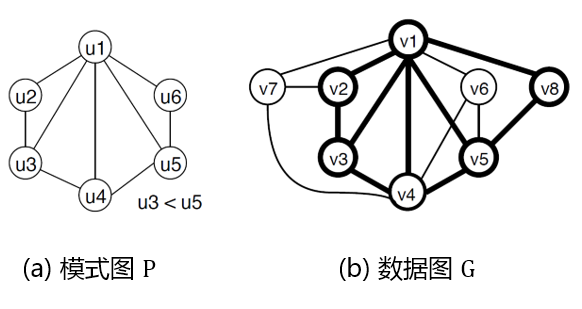
图3:子图匹配示例
实际应用案例中的数据图G可能非常大,拥有千万甚至上亿条边;而模式图P通常很小,只包含若干顶点和数条边。在规模巨大的数据图中查找较小的模式图,会产生非常多的匹配结果。图4中列出了常用的基准数据图的统计信息,|V|和|E|分别表示图的顶点数和边数。表中同时列出了常见的模式图(三角形、Clique-4和对角矩形)在这些基准数据图上的匹配结果数量。匹配结果的数量可能会上千倍于数据图的边数。

图4:常见模式图在基准数据图上的匹配数量
数量庞大的匹配结果导致子图枚举的计算量非常大,单机计算的时间将变得不可忍受。为了能处理大规模的数据图,分布式计算势在必行。目前已有多种针对不同分布式计算平台的子图枚举算法被提出,例如有基于Pregel的PSgL算法[1]、基于MapReduce的TwinTwig[2]、SEED[3]和CBF[4]算法等。
目前,性能最好的分布式子图枚举算法是基于MapReduce平台的CBF算法[4]和基于Timely Dataflow的BiGJoin算法[5]。这两个算法都是将子图匹配转换为分布式join的问题,从而利用MapReduce/Timely Dataflow解决。
基于分布式join的子图匹配算法会将模式图分解为一系列的基础join单元(例如三角形或边),如图5所示。join单元的子图匹配结果可以很容易地从数据图中匹配得到。基于分布式join的子图匹配算法首先会查找出所有join单元的部分匹配结果,然后将部分匹配结果在重合的顶点上进行join,从而得到整个模式图的匹配结果。
如果将子图匹配的结果用表的形式表示,则子图匹配的过程就是一系列的表之间的自然连接过程。因为子图匹配的结果数量很大,相应的表也会很大,可以天然地利用MapReduce来解决。
不同算法的区别在于基本join单元的定义和join框架。常用的基本join单元有edge、TwinTwig、star、clique和crystal,而常用的join框架有left deep join(TwinTwig算法), bushy join(SEED算法)和hash assembly(CBF算法)。
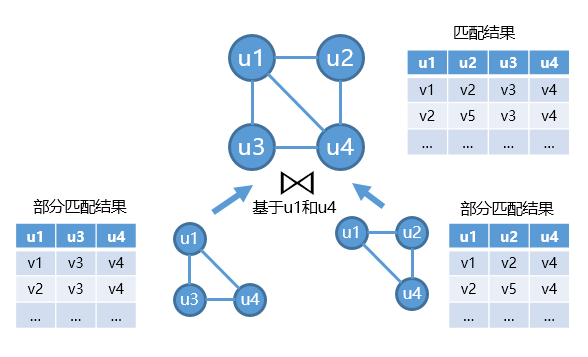
图5:基于分布式join的子图匹配算法
目前基于分布式join的子图枚举算法最大的痛点在于中间结果过多导致网络通信量过大。即使是小规模的基本join单元,在数据图上的匹配结果数量也大(如图4所示)。当模式图变得更加复杂时(如图6所示),整个中间匹配结果的数量将会达到10亿的级别。然而在分布式join的过程中,来自两张表的中间匹配结果需要经过shuffle才能join在一起。巨量的中间匹配结果使shuffle过程产生大量的磁盘和网络通信开销,变得非常昂贵。

图6:复杂的模式图
我们的工作试图从另一个角度去解决分布式子图匹配问题。我们发现中间匹配结果的大小远大于数据图,这启发我们考虑是否可以shuffle数据图而不是中间匹配结果?基于此,我们提出了BENU算法框架。
BENU算法框架采用了任务并行的思路,将数据图上的子图匹配问题转换为一系列的在数据图不同部分进行匹配结果搜索的任务。在分布式环境下,不同的机器并行地执行不同的搜索任务,各任务的搜索结果合并在一起就是全图的匹配结果,从而实现分布式子图匹配。
BENU的系统架构如图7所示。不同于之前的分布式算法,BENU同时利用了分布式计算平台和分布式key-value数据库。BENU利用分布式计算平台(例如Hadoop和Spark)完成搜索任务的并行执行,利用分布式数据库存储数据图。
BENU算法框架的伪代码如图8所示。在预处理步骤,BENU将数据图以邻接表的形式保存在一个分布式key-value数据库中,key为顶点ID,value为顶点的邻接表。针对用户给定的每个模式图P,BENU在driver端为P生成查询计划E,并将查询计划广播到集群的所有机器中。BENU为数据图中的每一个顶点生成一个搜索任务,搜索任务以该顶点为起点,在查询计划E的指导下在该顶点的邻域中搜索匹配结果。在任务的执行过程中,BENU按需地访问数据库以查询数据图顶点的邻接表。
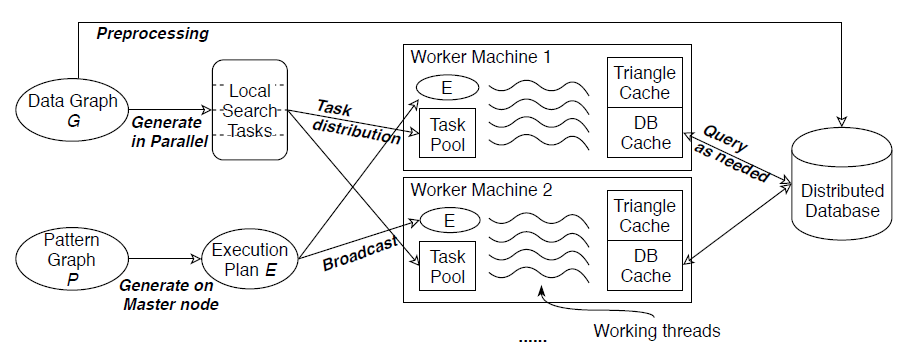
图7:BENU算法的系统架构

图8:BENU算法框架的伪代码
BENU查询计划是BENU的核心概念,查询计划具体地指导匹配子图的搜索过程。BENU查询计划基于回溯搜索框架。BENU为模式图中的所有顶点赋予一个全局固定的匹配顺序,并按照匹配顺序将模式图的顶点与数据图的顶点逐一地尝试配对。图9展示了逐顶点匹配的过程,其中u1和u3已经与v1和v3匹配,正在对u2进行匹配。当u2匹配失败时,即不能在数据图中找到一个合适的映射顶点而不影响图同构的正确性时,BENU查询计划会回溯到前一个成功匹配的顶点u3,再继续尝试将u3匹配到另一个数据图顶点。在匹配的过程中,查询计划会访问分布式数据库以获取数据图顶点的邻接表,从而确定下一步匹配的候选顶点集。
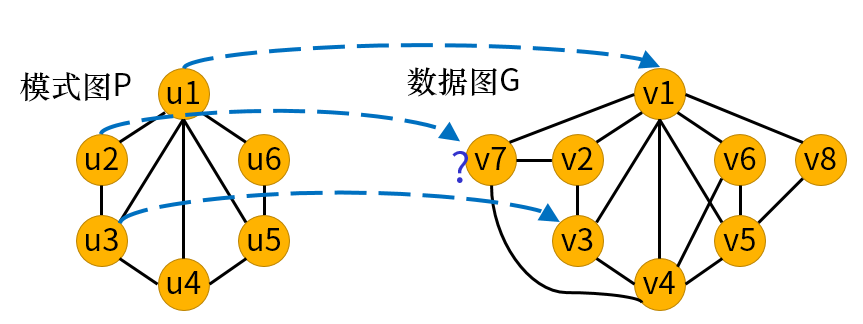
图9:基于回溯的逐顶点匹配过程示例(匹配顺序:u1,u3,u2,u5,u6,u4)
我们可以将上述回溯搜索的过程用一个抽象的程序表达。程序中定义了6种指令(如图10所示),每种指令对应于子图匹配中的一个基本操作。模式图查询的整个过程可以表达为一个如图11最左侧的Raw Execution Plan所示的程序。

图10:查询计划中使用到的指令

图11:查询计划与其优化
将子图匹配过程表达为程序,使我们可以从程序优化这个全新的角度,对子图匹配过程进行优化,进一步消除冗余计算。我们提出了公共子表达式消除、指令重排序、三角形缓存、查询结果压缩等四项优化技术,将图11中最左侧的查询计划优化为最右侧的查询计划。受限于篇幅,优化技术的细节在论文中有详细介绍。
除了在查询计划层面降低计算开销,我们又提出了数据库缓存和任务划分等系统层优化技巧。
我们发现同一个搜索任务在回溯搜索的过程中,同一个邻接表会被多次访问,呈现出任务内数据访问局部性的特性;而不同的搜索任务也可能会访问相同的邻接表,呈现出任务间数据访问局部性特征。为了充分利用局部性,我们在每个计算节点上创建了一个全内存的数据库缓存,保存从分布式数据库中获得的邻接表。通过采用LRU等缓存替换策略,数据库缓存可以有效捕获数据访问局部性。
对于某些高度数的顶点,其邻接表会非常大,导致从该顶点出发的搜索任务的执行开销显著大于其他搜索任务,造成负载不均衡。我们将高负载的搜索任务按照邻接表的范围进一步划分,将搜索任务拆分成子任务,分布在多台机器上执行,达到负载均衡。
我们在拥有1个主节点和16个计算节点的集群中对BENU算法进行了性能评估,本节摘录部分实验结果。BENU算法基于Hadoop MapReduce实现,采用HBase作为分布式数据库。
我们利用图6中所示的复杂模式图,对比了BENU算法与目前最好的两个分布式子图枚举算法CBF和BiGJoin的执行时间,结果如图12和图13所示。与CBF算法相比,几乎在所有的case下,BENU都比CBF执行速度快,在q2、q4和q6等模式图上,BENU比CBF能快一个数量级。

图12:BENU与CBF算法的性能对比。每个单元格的第一个数字是执行时间(秒),第二个数字是网络通信量(字节)
与基于Timely Dataflow的BiGJoin算法相比,在中规模数据集ok上,除了三角形之外,BENU比BiGJoin的两个版本都要快。在大规模数据集fs上,BiGJoin(S)因为内存溢出而崩溃,而BENU比BiGJoin(D)在所有的case上都要快。

图13:BENU与BiGJoin算法的执行时间对比。BiGJoin(S)和BiGJoin(D)分别表示BiGJoin算法的单机多线程以及分布式版本
数据库缓存对于BENU的性能有直接的影响。我们测量了随着缓存容量的提升,BENU算法的性能指标的变化情况,如图14所示。随着缓存容量的提升,缓存命中率大幅提升至90%以上,说明子图匹配计算拥有很强的数据局部性。数据库缓存有效地降低了BENU算法的网络通信量和执行时间。
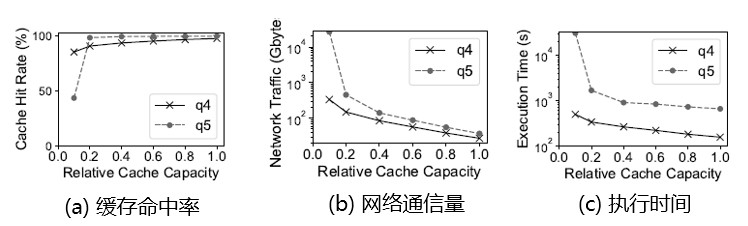
图14:相对缓存容量对性能指标的影响
我们也测量了BENU算法执行时间随着计算节点数的变化情况,如图15所示。随着计算节点数的增加,BENU算法呈现出了近似线性的节点可扩展性。
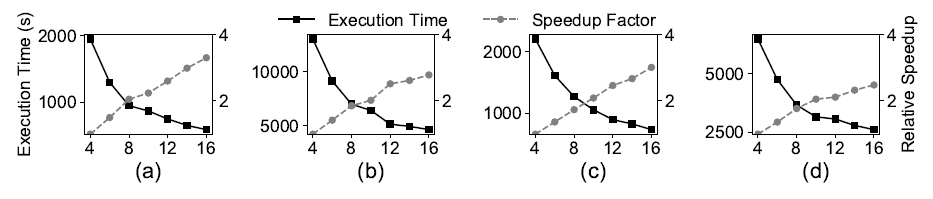
图15:BENU算法的节点扩展性实验结果
子图匹配作为图数据查询的核心技术之一,在图分析、图数据库领域扮演着越来越重要的角色。BENU算法聚焦于子图匹配的核心计算——无向图的子图同构匹配,通过任务并行和回溯框架相结合的方式,BENU算法大幅提高了分布式子图同构计算的性能。
未来,我们准备将BENU算法框架拓展到有向属性图模型上,利用BENU算法来大幅提高知识图谱和图数据库系统的查询性能。同时,我们希望将BENU算法应用于图模式Motif挖掘算法中,提升Motif挖掘的计算速度。
[1] Y. Shao, B. Cui, L. Chen, L. Ma, J. Yao, and N. Xu, “Parallel Subgraph Listing in a Large-scale Graph,” in Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data, 2014, pp. 625–636.
[2] L. Lai, L. Qin, X. Lin, and L. Chang, “Scalable Subgraph Enumeration in MapReduce,” Proc. VLDB Endow., vol. 8, no. 10, pp. 974–985, Jun. 2015.
[3] L. Lai, L. Qin, X. Lin, Y. Zhang, and L. Chang, “Scalable Distributed Subgraph Enumeration,” Proc. VLDB Endow., vol. 10, no. 3, pp. 217–228, 2016.
[4] M. Qiao, H. Zhang, and H. Cheng, “Subgraph matching: on compression and computation,” Proc. VLDB Endow., vol. 11, no. 2, pp. 176–188, Oct. 2017.
[5] K. Ammar, F. McSherry, S. Salihoglu, and M. Joglekar, “Distributed evaluation of subgraph queries using worst-case optimal low-memory dataflows,” Proc. VLDB Endow., vol. 11, no. 6, pp. 691–704, 2018.
